K-Armed Bandits

Jun 2021

Handout-10

May 2019

Inspired from Handout-10 , Source code: Github

Range minimum queries (RMQ)

E.g. we have an array A of length N, and we want to find the minimum element inside a subset of this array denoted by indices i and j, where 0 ≤ i ≤ j < N. The simple, out-of-the-box solution is to iterate over elements from indices i to j, and find the minimum. This has a runtime complexity of O(N), and no preprocessing time, i.e. O(1) runtime complexity.

However, if A is fixed/static, we can do some preprocessing such that we get better RMQ performance.

Let's define a pair of runtime complexities that quantify each RMQ solution:

• p(N) : runtime complexity of preprocessing.
• q(N) : runtime complexity of each RMQ.

In the simple solution with no preprocessing described above :

• p(N) = O(1).
• q(N) = O(N).

Another solution is to do complete preprocessing by building a lookup table for all possible RMQ on the static array A. Since i ≤ j, this will build an upper-triangular NxN matrix with a non-zero diagonal. Using dynamic programming (see implementations on project github page), we can build this with a runtime complexity of Θ(N²). Hence, for this solution, the runtime complexities are:

• p(N) = Θ(N²).
• q(N) = O(1).

See implementations here .

Anagram Checker

June 2017

Inspired from this Reddit thread , Source code: Github

Idea

Proposed algorithm to find if two input words are anagrams: Map each of the 26 english characters to a unique prime number. Then calculate the product of the string. Two strings are anagrams if and only if their products are the same. Let's call this approach PRIME.

Current best ways of doing the above, in order of popularity/performance:

1. Count frequency of each letter in each word, and then simply compare. If the strings are anagrams, the frequency bins will be identical. Let's call this approach FREQ.
2. Sort letters in each word. The resultant strings of each word will be exact. [NOT Implemented yet]

The proposed algorithm is arguably slower, and also susceptible to integer overflow. Will require 128-bit integer arithmetic at least to guarantee all words can be supported (Source )

But the following optimization might help practical use-case: Map primes efficiently to each letter by frequency of occurrence in the english language.. example, 'e' is the most frequently found alphabet in text, so map 'e' to the smallest prime number, i.e. 'e' = 2. Let's call this approach PRIME-ORD.

Some results

Some thoughts

Interestingly, the prime number approach is faster than the frequency-binning approach. This is kind of a testament to how well optimized integer arithmetic is on modern microprocessors. Ordering the primes doesn't seem to have any significant impact on performance, but you could argue that the two simple tests above are not enough to stress the processor. Longer strings, or larger number of solves might add up to deliver an overall benefit with the PRIME-ORD approach. In the future, a dictionary run on known anagrams (or some curated list of non-anagrams) could help test this theory. The sorting approach described above could also be implemented as a third option, but I doubt it would outperform the prime-multiplication approach on anagrams in the English language.

Which kind of brings me to some final thoughts... is there any use for this stuff? Anagram checking isn't exactly going to make the "Top 10 unsolved problems" list, but perhaps there is some esoteric use-case that I'm unaware of? I'll love to hear about it if you have any thoughts on this.

ASCII Art

September 2015

ASCII art is cool. And so, I wrote an image-to-ASCII converter. It's nothing novel really, but I thought I'll write one anyway as an exercise.

Since I have been doing a lot of R programming lately, I decided to use R to write the ASCII converter. Yes, I'm aware that it is not the ideal choice: more lines of code, and probably poorer performance. But these weren't really my concerns, and besides, on modern computers, I found that my code "ASCII-fied" images within minutes. This post is to share what I have made and explain how it works. All of the code and some accompanying examples can be found on GitHub here .

The code is an almost direct implementation of the content from this wonderful paper by Paul D. O’Grady and Scott T. Rickard titled Automatic ASCII Art Conversion of Binary Images Using Non-Negative Constraints. It can be found in the IET repositories here .

Right, so let's get started. I've divided this post into 3 key sections:

• Setup: What you need before you run the R code to convert the image to ASCII. e.g. generating glyphs from fonts, global constants, etc..
• ascii.R: Basically, the meat of this post. What the code is, how it's organized, and why it works.
• Results: The most visually appealing section of this post. Some of the ASCII-fied images, including the famous Lena!

1. SETUP

So the very first step is to decide on which font to use, which can be a little tricky (comic sans not even considered, for obvious reasons). The authors in the paper suggest using a monospace font, which makes sense and simplifies the problem. I end up using the same Courier monospace font used by the authors in their experiments.

The next step is to generate the glyphs from the font. Glyphs are basically individual characters; they could be a numeral, letter of the alphabet, punctuation, etc. Fonts are digital files that contain information on how to generate these characters (glyphs) in accordance to some common design styles (also known as the font's typeface). We can use the font-files to generate any supported glyphs as image files, which we will use to replace blocks of our original image when converting it to ASCII. We use 95 classic 7-bit-ASCII characters -- 26*2 = 52 alphabets (upper/lower-case), 10 numerals (0-9), 32 characters (just look down at your keyboard, and count the number of characters you can type out with/without the shift key. E.g. !@#$%^*), and the blank (white-space) character -- to generate the ASCII art. We could easily extend this to include the extended 8-bit ASCII set (includes special characters such as "é"), but for now, we limit ourselves to the 95 printable characters detailed above.

Anyways, the next question is how do we generate these glyph images from a font-file? Well, given that I have no background on this topic, I turned to the interwebs for a solution, and found a neat little Ruby script written by yukinoraru , which can be found on his/her GitHub repository here . The script is straightforward enough to use -- edit the source font-file you want to use, adjust the FONT_SIZE variable to desired size (I use "19x38"), and edit the FIRST and LAST variables (I use "\u0020" and "\u007e" respectively -- characters 32 to 126 in the ASCII table) to specify the start/end ASCII number for glyphs you want to generate. Running the script generates individual font-glyph image files based on your settings, and saves them as PNG files, named as their ASCII number (e.g. the "!" character is number 33 in the ASCII table, and would be generated as 33.png).

Eventually, for reasons I shall not go into, I end up using the JPG file format for all glyph and source images. You can easily convert the PNG glyph files from the above step to JPG using ImageMagick , or whatever suits your jimmies.

So far, we've made good progress -- we have 95 glyph images in the JPG format, and they are all extracted from the Courier monospace font library. We will convert our input (JPG) image file into an ASCII image that uses these 95 glyph images. I store these glyph images in the folder "Courier-Glyphs".

2. ASCII.R

This is where things get interesting, and where we actually start writing the ASCII converter (in R). Before I start sharing code snippets, however, let me try and give a very quick and intuitive description of how we are going to achieve this conversion. If you are interested to learn about the technique in greater detail, I recommend that you read the paper I mention above.

Basically, we are trying to approximate the input image using the available glyphs. The input image is broken up into 2D pixel-blocks, where each block is the same size as a glyph (I use "19x38" -- width x height). The goal is to find the closest glyph to replace each pixel-block, i.e. match glyphs with the closest 2D color-distribution of each pixel-block. The problem can be represented as a matrix equation:

V ≈ WH

We only need the R jpeg package, which we load by calling library(jpeg) at the beginning. We then define some global constants:

#declare global constants
num_glyphs <- 95
glyph_size <- 19*38
beta <- 2 #SED = 2, KLD = 1
epsilon <- 0 #threshold
num_iterations <- 500 #number of H update iterations

We then convert the input image to grayscale, using the luminosity method 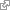. For a sanity check, if the input image is already in grayscale, we simply move on and set variable bw_img appropriately.

#read in image
img <- readJPEG("input.jpg")
if (length(dim(img)) == 3){
  #convert image to grayscale using luminosity method -- 0.21 R + 0.72 G + 0.07 B
  bw_img <- matrix(, nrow = nrow(img), ncol = ncol(img))
  for (i in 1:nrow(img)){
    for (j in 1:ncol(img)){
      bw_img[i,j] <- 0.21*img[i,j,1] + 0.72*img[i,j,2] + 0.07*img[i,j,3]
    }
  }  
} else {
  bw_img <- img
}

Now that we've read in the JPG image, and converted it to grayscale (if necessary), we have the matrix bw_img, which is simply grayscale values between 0 and 1, inclusive, for each pixel in the original image. We now need to break this 2D matrix structure into pixel-blocks, based on the size of the glyphs. The figure below shows how an image can be broken into pixel-blocks. In this case, the blocks are rather big, as we are breaking the image into only 16 blocks.

Each block is the size of one glyph, and hence will eventually be replaced by one character. At this point, it might seem silly that we are going to recreate Lena using only 16 ASCII characters, but bear with me. In practice, the blocks are of smaller size, and hence, giving us better resolution that produces a clearer ASCII image output.

Sidenote: if the input image size is not a nice multiple of glyph size, i.e. the image cannot be divided into a nice whole number of pixel-blocks, we can simply pad the original image with ones for any extra rows and columns. In grayscale, padding with one would just produce some inconspicuous extra whitespace in the final output ASCII image. I'm not going to explain how to "one pad" the image, it's fairly straightforward and you can look into the code to understand how I achieved it.

So how do we construct matrix V after we have broken the image into pixel-blocks? We simply take each pixel-block, unroll it as a column vector, and iteratively build matrix V one column at a time. So if we take the example figure of Lena above again, the dimensions of our matrix V would be (M*N) x 16, where (M*N) is number of rows of matrix V, and 16 is number of columns of matrix V. Why? When you unroll an image block, there would be M*N elements, resulting in a column-vector of length M*N. There would be 16 such pixel-blocks, hence, 16 columns in matrix V. Here is what the code looks like to construct matrix V:

g_row <- 38 #height of glyph = nrow(glyph_matrix) = N
g_col <- 19 #width of glyph = ncol(glyph_matrix) = M
P <- nrow(bw_img) #height of image
Q <- ncol(bw_img) #width of image
num_blocks_per_row <- P / g_row
num_blocks_per_col <- Q / g_col

V <- matrix(, nrow = g_row*g_col, ncol = num_blocks_per_row*num_blocks_per_col)
for (i in 1:num_blocks_per_row){
  for (j in 1:num_blocks_per_col){
    v <- vector()
    #construct column-vector of pixel-block
    for (x in 1:g_col){
      for (y in 1:g_row){
        v <- c(v,bw_img[(i-1)*g_row+y,(j-1)*g_col+x])
      }
    }   
    V[,(i-1)*num_blocks_per_col+j] <- v
  }
}

Note that P and Q are the dimensions of the image after it has been resized and one-padded, as described earlier.

Let's now construct matrix W using the 95 glyphs we generated in the section earlier.

#read in glyphs to construct the matrix W
W <- matrix(, ncol = num_glyphs, nrow = glyph_size)

glyphDir <- "./Courier-Glyphs/"
for (i in 32:126){ #32:126 --> numbering of glyph file name
  filename <- paste(glyphDir,i,".jpg",sep="")
  glyph <- readJPEG(filename)
  glyph <- as.vector(glyph) #column-wise unroll
  l2norm <- sqrt(sum(glyph^2))
  glyph <- glyph/l2norm
  W[,i-31] <- glyph
}

The intuition is the same here as well. We have glyph images, which are of size pixel-block. We can simply unroll each glyph as a column-vector, which gives us a set of possible columns we want to try and fit to reconstruct the original image. Matrix W, just like V, remains constant througout the runtime. Note that each glyph is rescaled by its L2-norm. This step is important, as it rescales the pixels to reflect a color-weight-distribution instead of raw pixel values. Since it is a winner-takes-all approach, the rescaling helps the convergence process. Finally, the dimensions of matrix W, referring back to the Lena example above again, would be (M*N) x 95, as there are 95 possible glyphs in our current implementation.

Alright, so we're almost done. We are left with the matrix H, which is the matrix that stores the weights, and is iteratively updated to refine the glyph selected for each pixel-block. The dimensions of matrix W is 95 * (number of image blocks), or 95 * 16 for the Lena example above. Each column has 95 rows, which represent weights to select one of the possible 95 glyphs. We have to update these weights iteratively for each column, which represent each of the pixel-blocks. The update function is the heart of this implementation, as it ultimately decides the performance of the converter. This, incidentally, was also the hardest, yet shortest (in number of lines of code), to write. Here is the mathematical formulation of the update function given in the paper:

Here is how I wrote it in R. Note that we update the H matrix for num_iterations specified above, and %*% is the matrix-multiplication operator in R. Also, W is initialized with random positive non-zero numbers.

for (t in 1:num_iterations){
  WH <- W %*% H    
  WH_num <- V/(WH^(2-beta))
  WH_den <- WH^(beta-1)
  H_next <- H * (t(W) %*% WH_num)/(t(W) %*% WH_den)
  H <- H_next
  #sanity check to make sure we don't get infinities/NaNs
  H_vec <- as.vector(H)
  H_vec[!is.finite(H_vec)] <- 0
  H <- matrix(H_vec,nrow = num_glyphs, ncol = num_blocks_per_row*num_blocks_per_col)
}

The hard part about this chunk of code was to express the mathematical formulation of the update function above as a bunch of single-shot linear algebra matrix operations (transpose, matrix-multiplication, etc). Once that mind-bending part was done, the code was rather straightforward and only required a few lines. I also initially wrote a naive serial version which updated H matrix values one-at-a-time, but that turned out to be extremely slow and inefficient. I've commented out that code in the final version, but if you're interested, you can have a look and see why and how nested for-loops with irregular memory access patterns can kill performance. Functionally, both update implementations produce identical results.

And voila, that is pretty much it. The final steps are pretty easy, so I won't spend too much space explaining them. Once all the desired number of iterations have finished, you identify the maximum H value in each column. The row-index of the maximum value in each column is the glyph number that you should use to replace that particular pixel-block from the original image. Doing this for all pixel-blocks, you will end up reconstructing the original image using ASCII characters. You just have to be careful that you reconstruct the image in the exact reverse order in which you constructed matrix V. Then, once you have the reconstructed matrix, you can write it out as a JPG file using the jpeg R package!

3. RESULTS

As mentioned above, I use the SED cost function, and hence, the beta variable is set to 2 for the results shown in this section. I also found that I needed to run a fair number of iterations to get better results. Usually, more than 100 iterations would do, but for large images, I ran at least 500 iterations to get appealing results. If you find that your output image, instead of whitespace, is selecting underscores (_) or dashes (-), then you probably need to run the converter for more number of iterations. Also, because of the size of the glyphs (19*38), I realized that the input image has to be rather large to get accurate results. Stick to images that are at least approximately 1000x1000 pixels in size.

Lena (Original)	Lena (ASCII)
Homer (Original)	Homer (ASCII)
Homer 2 (Original)	Homer 2 (ASCII)
.. and the scariest one of them all...
Jennifer Aniston (Original)	Jennifer Aniston (ASCII)

Well, that's all there is to this post for now. Hope you enjoyed the little tutorial, and if you have any questions, feel free to contact me!

CREDITS

Hilite.me